9-2-6. 型付素性構造の詳細
型とその階層
型は継承関係によって定義された階層構造を備えています。
図 1 では、三角形の種類についての型階層を表現しています。
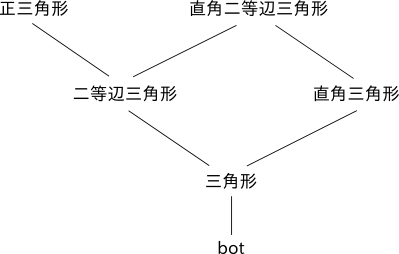
図 1 三角形の階層関係
型の継承関係が線のつながりで表されています。例えば、二等辺三角形と直角三角形はどちらも三角形を継承しています。型が表す概念としては、上側に 行くほど特殊性が増し、下側に行くほど一般性が増しています。ある型を基準に、そこから線でたどれる上側の型 (自分自身を含む) を subtype と呼び、下側の型 (自分自身を含む) を supertype と呼びます。例えば正三角形は三角形の subtype となります。複数の型を継承することもできます。例えば、直角二等辺三角形は二等辺三角形と直角三角形の両方を継承しています。
このように、型階層を用いて概念の階層関係を表現することができます。一番下にある bot という型 (bottom の意味) は、最も一般的な型であり、すべての型は bot の subtype となります。
型の定義と記述
型を用いるためにはあらかじめ型定義を行っておく必要があります。
型定義は次のような書式で行います (素性を持つ型の定義方法は後で示します) 。
型 <- [型1, 型2, ...].
左辺の型が継承先、右辺の型が継承元です。型名として用いることのできる文字列の種類は、アトムに用いることのできるものと同一です。
右辺の型は、bot のような組み込み型を除き、すでに定義されている必要があります。つまり、型定義においては、上のほうの行で一般性の高い型を定義し、下に行くほど特殊性の高い型を定義することになります。
同じ型は 2 度宣言することはできません。左辺に同じ型が 2 度以上出現するとエラーになります。
型定義はトップレベルから行うことはできません。ファイル中に記述しコンサルトする必要があります。
図 1 の三角形の階層構造を AZ-Prolog で宣言すると以下のようになります。
三角形 <- [bot]. 二等辺三角形 <- [三角形]. 直角三角形 <- [三角形]. 直角二等辺三角形 <- [二等辺三角形, 直角三角形]. 正三角形 <- [二等辺三角形].
プログラム中で型を表すには、型名の後に '&' を付与します。たとえば、二等辺三角形の型は
二等辺三角形&
と表記されます。'&' が付与されない場合は単なるアトムとして解釈されます。なお、
二等辺三角形& = X.
などのように、型の直後に演算子を書く場合は、'&' と演算子の間にスペースを入れる必要があります。スペースを入れずに '&=' と書くと、まとまった単独の演算子として解釈されてしまいます。ただし、
X = 二等辺三角形&, X = 直角三角形&.
のような場合に登場する '&,' や '&.' という表記に関しては例外で、それぞれ '&' と ',' および '&' と '.' の 2 つの演算子の並びとして扱われます (fs_mode/2 述語で素性構造モードを 2 に指定した場合) 。つまり、上の例は
X = 二等辺三角形& , X = 直角三角形& .
と等価です。
型の単一化
型どうしの単一化とは、共通の subtype の中で最も一般的な型 を見つける処理に相当します。
先ほどの三角形の例でいえば、二等辺三角形と直角三角形を単一化すると直角二等辺三角形が得られます。三角形と二等辺三角形を単一化すると二等辺三角形が得られます。正三角形と直角三角形は共通の subtype を持たないため、この 2 つの型は単一化に失敗します。
| ?- X = 二等辺三角形&, X = 直角三角形&.
X = 直角二等辺三角形&{}.
yes
| ?- X = 三角形&, X = 二等辺三角形&.
X = 二等辺三角形&{}.
yes
| ?- X = 正三角形&, X = 直角三角形&.
no
単一化した結果に {} が付いているのは、後述する型推論によるものです。
型階層を定義する際には、単一化した後の型は一意に決まるようにする必要があります。
図 2a において、 c と d はともに a と b の共通の subtype ですが、 c と d の間に継承関係は存在しないため、最も一般性を持つ subtype が決定できません。そのため、 a と b を単一化した結果となる型が一意に定まりません。このような階層構造は定義エラーとなります。
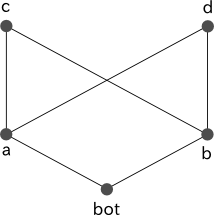
図 2a
% 図 2a に対応する型定義 a <- [bot]. b <- [bot]. c <- [a, b]. d <- [a, b].
c と d をともに a と b の共通の subtype としたい場合には、図 2b のように、まず e を、 a と b の唯一の単一化先として導入し、この e から c と d を継承するように定義する必要があります。
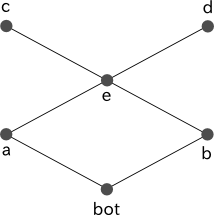
図 2b
% 図 2b に対応する型定義 a <- [bot]. b <- [bot]. e <- [a, b]. c <- e. d <- e.
図 3 においては、b と c、 あるいは a と d などに関しては単一化の結果は一意に定まります。しかし、 a と b に関しては共通の subtype である e と f のうち、どちらがより一般性を持つか比較不可能なため、単一化する型が決定できません。
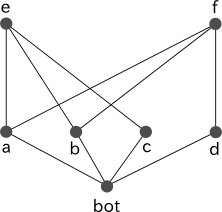
図 3
% 図 3 に対応する型定義 a <- [bot]. b <- [bot]. c <- [bot]. d <- [bot]. e <- [a, b, c]. f <- [a, b, d].
図 4 において a の直接の子は c と f であり、b の直接の子は d と e なので、これらの間に共通する型はありませんが、さらに継承関係をたどってみると、e と f がともに a と b の共通の subtype であることが分かります。しかし、e と f の間に階層の上下関係がなく、より一般的な型が決定できないため、このような階層構造は不適切です。
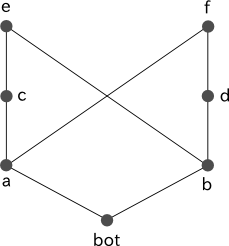
図 4
% 図 4 に対応する型定義 a <- [bot]. b <- [bot]. c <- [a]. d <- [b]. e <- [b, c]. f <- [a, d].
単一化先が 1 つしか存在できないということは、単一化によるバックトラックは必然的に発生しないことを意味します。
組み込み型
bot, list, string, atom, integer, float
bot 型は、前述のとおり、すべての型の supertype となる型です。list 型、string 型、atom 型、integer 型、 float 型はそれぞれ任意のリスト、文字列、アトム、整数、実数に対応する型です (後で述べるように、素性の値の指定に用いられます) 。
素性
次の書式を用いて、型に任意の項を持たせることができます。
型&項
項が素性構造の場合、素性構造の中の素性とペアとなる値もまた型を持ちますが、これも同様に任意の項を持つことができるため、入れ子構造を作ることができます。これを型付素性構造と呼びます。
素性構造の表記法など、基本的な仕様は型のない素性構造と同じです。ただし、型が持つ素性構造においてはその型で定義された素性以外を使うことはできません。また、素性構造内において、素性とペアになる値に与えることのできる型は、素性の定義の際に指定された型と単一化されるものに限られます。
型付素性構造は次の書式で表されます。
型&{素性1:素性1の値, 素性2:素性2の値, ...}
以下に示すのは、入れ子状になった型付素性構造の例です。
油彩画&{作品名:星月夜,
作者:人物&{名前:フィンセント・ファン・ゴッホ,
出身地:オランダ&},
制作年:1889,
展示場所:施設&{施設名:ニューヨーク近代美術館,
所在地:ニューヨーク州&}}
これは全体として「油彩画」型の値を持ちます。素性の値に登場する「人物」「施設」「オランダ」「ニューヨーク州」も型となっています。「フィンセント・ファン・ゴッホ」「ニューヨーク近代美術館」はアトムであり、"1889" は整数です。
型付素性構造を使用するためには、 fs_mode/2 述語を用いて、素性構造モードを型付素性構造モードに切り替える必要があります。ただし、型定義を含むファイルをコンサルトした時点で、この切り替えは自動的に行われます。
型付素性構造は、型のない素性構造の場合と同様に、 fs_writeAVM/1 述語を用いて AVM 形式で出力することができます。
<例>
| ?- X = 彫刻&{作品名:ミロのヴィーナス,展示場所:施設&{施設名:ルーヴル美術館,所在地:フランス&}}, fs_writeAVM(X).
|~彫刻 ~|
| 作品名: ミロのヴィーナス |
| 作者: 人物 |
| 制作年: integer |
| 展示場所:|~施設 ~| |
| | 所在地:フランス& | |
| | 施設名:ルーヴル美術館 | |
| |_ _| |
|_ _|
X = 彫刻&{作品名:ミロのヴィーナス,展示場所:施設&{施設名:ルーヴル美術館,所在地:フランス&}}.
yes
型付素性構造が AVM 形式で出力される際には、最初に型についての情報が表示された後、素性とその値が列挙されます。
素性を持つ型の定義
素性を用いるためには、あらかじめ素性を定義しておく必要があります。
素性の定義は、型定義に加えて、素性と素性が持つ型のペアを列挙することで行われます。
型 <- [型1, 型2, ...] + [素性1:素性1の型, 素性2:素性2の型, ...].
素性名として用いることのできる文字列の種類は、アトムに用いることのできるものと同一です。ある型で定義した素性は、それを継承した型でも引き継がれます。素性を定義した型の subtype 以外では同じ素性を用いることはできません。
先ほどの美術品の例のような素性構造を定義するためには、例えば以下のような宣言が必要になります。
場所 <- [bot]. ヨーロッパ <- [場所]. オランダ <- [ヨーロッパ]. フランス <- [ヨーロッパ]. 北米 <- [場所]. アメリカ合衆国 <- [北米]. ニューヨーク州 <- [アメリカ合衆国]. 人物 <- [bot] + [名前:atom, 出身地:場所]. 施設 <- [bot] + [施設名:atom, 所在地:場所]. 美術品 <- [bot] + [作品名:atom, 作者:人物, 制作年:integer, 展示場所:施設]. 油彩画 <- [美術品]. 彫刻 <- [美術品].
素性がとることのできる値は、素性定義の際に指定した型とその subtype に限られます。例えば、素性「出身地」は「場所」型とその subtype だけを値として持つことができます。素性の型に組み込み型を指定した場合、素性がとることのできる値は、組み込み型が定めた値のみに制約されます。例え ば、素性「制作年」が取ることのできる値は整数のみになります。
素性の型を組み込み型の list 型とすることで、複数の値を列挙することができます。
<例>
% 型と素性の定義 s <- [bot]. t <- [bot] + [f:list].
以下では、素性 f の値は数字、アトム、s 型からなるリストとなります。
| ?- X = t&{f:[12345, abcdefgh, s&]}, fs_writeAVM(X).
|~t ~|
| f: [ |
| 12345 |
| ,abcdefgh |
| ,s& |
| ] |
|_ _|
X = t&{f:[12345,abcdefgh,s&]}.
yes
素性は原則として一度しか定義できません。ただし、ある素性を持つ型から継承して、その subtype の定義を行う際に、同じ素性を再定義し、素性が持つ値の制約を強めることは可能です。具体的には、素性の値の型を、当初定義されたものの subtype に更新する記述が可能です。
<例>
animal <- [bot] + [father:animal, mother:animal]. dog <- [animal] + [father:dog, mother:dog].
この場合、animal 型が持つ素性 father と mother は animal 型ですが、これを継承した dog 型が持つ素性 father と mother がとれるのは dog 型のみです。
素性を持つ型の単一化
型付素性構造どうしの単一化においては、まず型の単一化が行われ、それに成功すると続いて対応する素性どうしの単一化が行われます。これを再帰的に繰り返していき、どの単一化も失敗することなく完了すれば、型付素性構造の全体が単一化されたことになります。
<例>
% 型と素性の定義 香辛料 <- [bot]. わさび <- [香辛料]. 唐辛子 <- [香辛料]. 一味唐辛子 <- [唐辛子]. 七味唐辛子 <- [唐辛子]. 麺類 <- [bot] + [薬味:香辛料, 価格:integer]. そば <- [麺類]. 冷やしそば <- [そば]. きつねそば <- [そば]. 月見そば <- [そば]. 冷やしきつねそば <- [冷やしそば, きつねそば]. 冷やし月見そば <- [冷やしそば, 月見そば]. うどん <- [麺類].
型が単一化でき、素性の値の型も単一化できる場合
| ?- X = 冷やしそば&{薬味:一味唐辛子&}, X = きつねそば&{薬味:唐辛子&}.
X = 冷やしきつねそば&{薬味:一味唐辛子&{}}.
yes
型が単一化できない場合
| ?- X = 冷やしそば&{薬味:唐辛子&}, X = うどん&{薬味:唐辛子&}.
no
型は単一化できるが、素性の値の型が単一化できない場合
| ?- X = 月見そば&{薬味:七味唐辛子&}, X = そば&{薬味:わさび&}.
no
型が単一化でき、片方には対応する素性が存在しないような場合
| ?- X = きつねそば&{薬味:一味唐辛子&}, X = そば&{価格:700}.
X = きつねそば&{薬味:一味唐辛子&{}, 価格:700}.
yes
一方の型付素性構造が持つ素性とその値が、もう一方の型付素性構造には存在しない場合、存在する側の素性とその値が単一化先に引き継がれます。
型推論
AZ-Prolog ではコンサルトの際、およびトップレベルからの入力を評価する際に素性構造に対し型推論および型検査を行います (素性構造モードが型付素性構造モードのとき) 。
型のみで素性構造を備えていない場合、空の素性構造が付与されます。型情報が省略された素性構造には、推論により自動的に型が補われます。また、型と素性の対応、および素性と素性値の対応が、定められた制約を満たしているか検査されます。型検査の結果、エラーが生じなければ型推論によって適切な型に変換されます。
以下に、型推論および型検査の具体的な手順を示します。なお、以降の例においては次のような型定義が前もってなされていると仮定しています。
% 型と素性の定義 (型推論のすべての例で共通) 職業 <- [bot]. 農家 <- [職業] + [作物:atom]. 漁師 <- [職業] + [漁船数:integer]. 医者 <- [職業] + [診療科:atom]. プログラミング言語 <- [bot]. 'C言語' <- [プログラミング言語]. 外国語 <- [bot]. 英語 <- [外国語]. 通訳 <- [職業] + [通訳言語:外国語].
1.型のみが与えられており素性構造が付与されていない場合には、(素性値を持たない) 型付素性構造に変換されます。
<例>
t1 :- X = 職業&, write(X), nl.
(実行結果)
| ?- t1.
職業&{}
yes
2.型を持たない素性構造の場合、素性を参照し、その素性を定義している型が発見できたら、素性構造にその型を割り当てます。型の候補が複数存在するときは、その中で最も一般的な型を割り当てます。与えられた素性を定義している型が見つからない場合や、素性の組み合わせ方に不整合があり、型が決定できない場合にはエラーとなります。
<例>
推論で型が補われる場合
t2 :- X = {作物:トウモロコシ}, write(X), nl.
(実行結果)
| ? - t2.
農家&{作物:トウモロコシ}
yes
素性と関連付けられた型が存在しない場合
t3 :- X = {科目:音楽}, write(X), nl. % コンサルト時エラー
素性構造内のすべての素性と関連付けられた型が存在しない場合
t4 :- X = {漁船数:5, 診療科:外科}, write(X), nl. % コンサルト時エラー
3.型を持つ素性構造の場合も、まず素性構造だけを手がかりに型推論を行います。その上で、推論によって得られた型とプログラムに記述された型を単一化し、その結果となる型を割り当てます。単一化に失敗すればエラーとなります。
<例>
与えた型と素性から推論した型に矛盾がない場合
t5 :- X = 漁師&{漁船数:2}, write(X), nl.
(実行結果)
| ?- t5.
漁師&{漁船数:2}
yes
t6 :- X = 職業&{漁船数:2}, write(X), nl.
(実行結果)
| ?- t6.
漁師&{漁船数:2}
yes
与えた型と推論した型が単一化できない場合
t7 :- X = 医者&{作物:ブドウ}, write(X), nl. % コンサルト時エラー
4.型が確定したら、次にそれぞれの素性に対して、素性値の型推論を行います。素性定義の際に素性値に与えた型を調べ、これをプログラム中の素性値の型と単一化します。単一化に成功すれば、その結果となる型で素性値を置き換えます (プログラム中の素性値が素性定義で与えた型の subtype ならば値は不変です) 。単一化に失敗すればエラーとなります。素性定義において組み込み型が与えられていた場合は、それに対応する値を素性が持っているかどうか検査します。
<例>
素性値の型と素性値がとりうる型とが矛盾しない場合
t8 :- X = 通訳&{通訳言語:英語&}, write(X), nl.
(実行結果)
| ?- t8.
通訳&{通訳言語:英語&{}}
yes
素性値の型が素性値がとりうる型ではない場合
t9 :- X = 通訳&{通訳言語:'C言語'&}. % コンサルト時エラー
素性値が組み込み型が指定する種類の値ではない場合
t10 :- X = 漁師&{漁船数:トロール漁船}. % コンサルト時エラー5.素性構造が入れ子状になっている場合には、上の手順を内側の素性構造に対して再帰的に実行し、すべての型推論および型検査が問題なく完了すれば成功となります。
構造共有
以下の例において、p(X) が真となるような X においては、本人の出生地と母親の現在地が必ず等しくなります。同様に、q(X) が真となるような X においては、本人の出生地と本人の現在地が必ず等しくなります。
人 <- [bot] + [出生地:atom, 現在地:atom, 父親:人, 母親:人].
p(人&{出生地:L, 現在地:岩手県, 母親:人&{現在地:L}}).
q(人&{出生地:L, 現在地:L}).
型付素性構造では、複数の素性が同一の値を指し示す場合があります。これを構造共有と呼びます。
| ?- p(X), fs_writeAVM(X).
|~人 ~|
| 出生地:_58 |
| 母親: |~人 ~| |
| | 出生地:atom | |
| | 母親: 人 | |
| | 父親: 人 | |
| | 現在地:_58 | |
| |_ _| |
| 父親: 人 |
| 現在地:岩手県 |
|_ _|
X = 人&{出生地:_58,現在地:岩手県,母親:人&{現在地:_58}}.
yes
| ?- q(X), fs_writeAVM(X).
|~人 ~|
| 出生地:_40 |
| 母親: 人 |
| 父親: 人 |
| 現在地:_40 |
|_ _|
X = 人&{出生地:_40,現在地:_40}.
yes
単一化においては、それぞれの素性構造での構造共有の情報も伝えられます。従って、 p(X) と q(X) が同時に成り立つような X においては、「本人の出生地と母親の現在地が等しい」「本人の出生地と本人の現在地が等しい」の両方が同時に成立することになり、結果として次のような素 性構造が得られます。
| ? -p(X), q(X), fs_writeAVM(X).
|~人 ~|
| 出生地:岩手県 |
| 母親: |~人 ~| |
| | 出生地:atom | |
| | 母親: 人 | |
| | 父親: 人 | |
| | 現在地:岩手県 | |
| |_ _| |
| 父親: 人 |
| 現在地:岩手県 |
|_ _|
X = 人&{出生地:岩手県,現在地:岩手県,母親:人&{現在地:岩手県}}.
yes
自然言語処理への応用
ここでは、文法理論の一種である HPSG を用いた日本語の簡潔な解析例を示します。
HPSG は、個々の語彙に文法に関する制約が記され、単一化を通じて制約条件を満たすように句の形成が行われるという特徴を持つ理論です。
言語学的な情報が格納される基本的な単位となるのが sign 型の値です。ここには、音韻や統語、あるいは意味に関する情報などが含まれます (この例では意味情報は省略しています) 。sign 型の subtype として word 型、 phrase 型があり、それぞれ単語と句に対応します。
例として、「きつねが転ぶ」という文を解析してみます。
単語「きつね」に対応する型付素性構造は次のようになります (説明のため、 AVM は AZ-Prolog で出力される形式と多少異なる点があります) 。
|~word ~| | PHONOLOGY:[きつね] | | SYN: |~gram_cat ~| | | | HEAD: 名詞& | | | | COMPS:[] | | | |_ _| | |_ _|
格助詞「が」に対応する型付素性構造は以下の通りです。
|~word ~| | PHONOLOGY:[が] | | SYN: |~gram_cat ~| | | | HEAD: |~格助詞 ~| | | | | | FORM:が格& | | | | | |_ _| | | | | COMPS: [ | | | | |~sign ~| | | | | | PHONOLOGY:list | | | | | | SYN: |~gram_cat ~| | | | | | | | HEAD: 名詞& | | | | | | | | COMPS:[] | | | | | | | |_ _| | | | | | |_ _| | | | | ] | | | |_ _| | |_ _|
素性 PHONOLOGY は音韻に関する情報を表します。この例では語を表記の通りに格納することにします。
素性 SYN は gram_cat 型の値をとり、統語論的情報を格納します。gram_cat 型は素性 HEAD と素性 COMPS を持ちます。
素性 COMPS のリストには、とるべき補語が示されています。格助詞「が」の場合、素性 SYN の素性 COMPS は、名詞を表す sign 型の値を 1 つ持つリストです。したがって、格助詞「が」は、名詞「きつね」を補語としてとることで、次のような句を形成することができます。
|~phrase ~| | PHONOLOGY:[きつね,が] | | SYN: |~gram_cat ~| | | | HEAD: |~格助詞 ~| | | | | | FORM:が格& | | | | | |_ _| | | | | COMPS:[] | | | |_ _| | |_ _|
単語ではなく句を意味する素性構造なので、型は phrase 型になっています。
素性 PHONOLOGY から分かるように、これは「きつねが」に対応する句です。ここでは、素性 COMPS は空リストとなっています。すでに名詞「きつね」が補なわれたため、これ以上は語を補う必要がないことを示しています。補語に関する規則は、末尾に掲載したプログラムにおいて head_complement_schema 述語に記述されています。
次に、素性 SYN の素性 HEAD を見てみると、「格助詞」型となっています。ここには主辞 (head) の情報が納められています。主辞とは、句の中心的な文法的性質を決定する語です。句「きつねが」においては、格助詞「が」が主辞となっています。このため、格助詞「が」の素性 HEAD から句「きつねが」の素性 HEAD へと情報が引き継がれたのです。この規則を記述しているのが head_feature_principle 述語です。
このようにして、語彙に記された情報を手掛かりに、2 つの単語を組み合わせて句を形成することができました。
続いて、動詞「転ぶ」の素性構造を以下に示します。
|~word ~| | PHONOLOGY:[転ぶ] | | SYN: |~gram_cat ~| | | | HEAD: |~動詞 ~| | | | | | FORM:終止& | | | | | |_ _| | | | | COMPS: [ | | | | |~sign ~| | | | | | PHONOLOGY:list | | | | | | SYN: |~gram_cat ~| | | | | | | | HEAD: |~格助詞 ~| | | | | | | | | | FORM:が格& | | | | | | | | | |_ _| | | | | | | | | COMPS:list | | | | | | | |_ _| | | | | | |_ _| | | | | ] | | | |_ _| | |_ _|
先ほどと同様に考えて、素性 COMPS を確認すると「が格」の「格助詞」型の文法的性質を持つ値を補語として持つことが分かります。先ほどの句「きつねが」はこの条件を満たしていますから、「転ぶ」は「きつねが」を補語として取り、全体として次のような句を形成します。
|~phrase ~| | PHONOLOGY:[きつね,が,転ぶ] | | SYN: |~gram_cat ~| | | | HEAD: |~動詞 ~| | | | | | FORM:終止& | | | | | |_ _| | | | | COMPS:[] | | | |_ _| | |_ _|
日本語の完全な文の場合、主辞の値は終止形の動詞型が来ること、および補語がこれ以上満たされる必要がないことが要請されます (述語 root_condition がこれに対応する制約を与えています)。上の素性構造はこれを満たしています。
これで、文「きつねが転ぶ」の解析が完了しました。
実際のプログラムにおいては、構文木の親子関係に関する規則を処理したり、解析結果を保存したりするために素性 DTRS, HEAD_DTR, COMP_DTR を用いています。解析が終わると、構文木の根にあたる素性構造の素性 DTRS に全体の構文木が格納されています。詳しくはプログラムを実行して確認してください。
%%%%%%%%%%%%%%%
% HPSG types %%
%%%%%%%%%%%%%%%
form<-[bot].
fin_form<-[form].
verb_form<-[form].
終止<-[verb_form,fin_form].
未然<-[verb_form].
case_form<-[fin_form].
が格<-[case_form].
に格<-[case_form].
を格<-[case_form].
の格<-[case_form].
pos<-[bot]+['FORM':form].
動詞<-[pos].
格助詞<-[pos].
名詞<-[pos].
形容詞<-[pos].
gram_cat<-[bot]+['HEAD':pos,'COMPS':list].
head_struc<-[bot]+['HEAD_DTR':bot].
head_comp_struc<-[head_struc]+['COMP_DTR':bot].
sign<-[bot]+['PHONOLOGY':list,'SYN':gram_cat].
phrase<-[sign]+['DTRS':head_struc].
word<-[sign].
%%%%%%%%%%%%%%%%
% HPSG parser %%
%%%%%%%%%%%%%%%%
parse([X|Rest],Rest,_,Lex):-
lexicon(X,Lex).
parse(L1,L2,[_|X],Tree):-
parse(L1,L3,X,T1),
parse(L3,L2,X,T2),
principles(T1,T2,Tree).
input_phrase(PHRASE,TREE):-
parse(PHRASE,[],PHRASE,TREE).
input(SENTENCE,TREE):-
root_condition(TREE),
input_phrase(SENTENCE,TREE).
%%%%%
test_sentences(1,[きつね,が,転ぶ]).
test_sentences(2,[きつね,が,山,に,住む]).
test_sentences(3,[きつね,が,とんび,に,油揚げ,を,買わ,ない]).
test_sentences(4,[油揚げ,が,とんび,に,取ら,れる]).
test(N,Y):- test_sentences(N,X),input(X,Y),!,fs_writeAVM(Y).
%%%%%%%%%%%%%%%%
%% principles %%
%%%%%%%%%%%%%%%%
head_complement_schema(LEFT,RIGHT,HEAD,COMP,MOTHER):-
MOTHER={'SYN':{'COMPS':COMPS},'DTRS':{'HEAD_DTR':HEAD,'COMP_DTR':COMP}},
HEAD={'SYN':{'COMPS':[COMP|COMPS]}},
LEFT=COMP,
RIGHT=HEAD.
id_principle(LEFT,RIGHT,HEAD,COMP,MOTHER):-
head_complement_schema(LEFT,RIGHT,HEAD,COMP,MOTHER).
head_feature_principle(HEAD,MOTHER):-
MOTHER={'SYN':{'HEAD':X}},
HEAD={'SYN':{'HEAD':X}}.
phonology_principle(LEFT,RIGHT,MOTHER):-
LEFT={'PHONOLOGY':X},
RIGHT={'PHONOLOGY':Y},
MOTHER={'PHONOLOGY':Z},
append(X,Y,Z).
principles(LEFT,RIGHT,MOTHER):-
id_principle(LEFT,RIGHT,HEAD,_,MOTHER),
phonology_principle(LEFT,RIGHT,MOTHER),
head_feature_principle(HEAD,MOTHER).
root_condition({'SYN':{'HEAD':動詞&{'FORM':fin_form&},'COMPS':[]}}).
%%%%%%%%%%%%%
%% lexicon %%
%%%%%%%%%%%%%
noun_phrase({'SYN':{'HEAD':名詞&,'COMPS':[]}}).
lexicon(きつね,
word&{'PHONOLOGY':[きつね],'SYN':{'HEAD':名詞&,'COMPS':[]}}).
lexicon(山,
word&{'PHONOLOGY':[山],'SYN':{'HEAD':名詞&,'COMPS':[]}}).
lexicon(とんび,
word&{'PHONOLOGY':[とんび],'SYN':{'HEAD':名詞&,'COMPS':[]}}).
lexicon(油揚げ,
word&{'PHONOLOGY':[油揚げ],'SYN':{'HEAD':名詞&,'COMPS':[]}}).
lexicon(に,
word&{'PHONOLOGY':[に],'SYN':{'HEAD':格助詞&{'FORM':に格&},'COMPS':[NP]}})
:- noun_phrase(NP).
lexicon(が,
word&{'PHONOLOGY':[が],'SYN':{'HEAD':格助詞&{'FORM':が格&},'COMPS':[NP]}})
:- noun_phrase(NP).
lexicon(を,
word&{'PHONOLOGY':[を],'SYN':{'HEAD':格助詞&{'FORM':を格&},'COMPS':[NP]}})
:- noun_phrase(NP).
lexicon(住む,
word&{'PHONOLOGY':[住む],
'SYN':{'HEAD':動詞&{'FORM':終止&},
'COMPS':[{'SYN':{'HEAD':格助詞&{'FORM':に格&}}},
{'SYN':{'HEAD':格助詞&{'FORM':が格&}}}] }}).
lexicon(買う,
word&{'PHONOLOGY':[買う],
'SYN':{'HEAD':動詞&{'FORM':終止&},
'COMPS':[{'SYN':{'HEAD':格助詞&{'FORM':を格&}}},
{'SYN':{'HEAD':格助詞&{'FORM':に格&}}},
{'SYN':{'HEAD':格助詞&{'FORM':が格&}}}] }}).
lexicon(買わ,
word&{'PHONOLOGY':[買わ],
'SYN':{'HEAD':動詞&{'FORM':未然&},
'COMPS':[{'SYN':{'HEAD':格助詞&{'FORM':を格&}}},
{'SYN':{'HEAD':格助詞&{'FORM':に格&}}},
{'SYN':{'HEAD':格助詞&{'FORM':が格&}}}] }}).
lexicon(取る,
word&{'PHONOLOGY':[取る],
'SYN':{'HEAD':動詞&{'FORM':終止&},
'COMPS':[{'SYN':{'HEAD':格助詞&{'FORM':を格&}}},
{'SYN':{'HEAD':格助詞&{'FORM':が格&}}}] }}).
lexicon(取ら,
word&{'PHONOLOGY':[取ら],
'SYN':{'HEAD':動詞&{'FORM':未然&},
'COMPS':[{'SYN':{'HEAD':格助詞&{'FORM':を格&}}},
{'SYN':{'HEAD':格助詞&{'FORM':が格&}}}] }}).
lexicon(取ら,
word&{'PHONOLOGY':[取ら],
'SYN':{'HEAD':動詞&{'FORM':未然&},
'COMPS':[{'SYN':{'HEAD':格助詞&{'FORM':に格&}}},
{'SYN':{'HEAD':格助詞&{'FORM':が格&}}}] }}).
lexicon(転ぶ,
word&{'PHONOLOGY':[転ぶ],
'SYN':{'HEAD':動詞&{'FORM':終止&},
'COMPS':[{'SYN':{'HEAD':格助詞&{'FORM':が格&}}}] }}).
lexicon(ない,
word&{'PHONOLOGY':[ない],
'SYN':{'HEAD':動詞&{'FORM':終止&},
'COMPS':[{'SYN':{'HEAD':動詞&{'FORM':未然&},'COMPS':COMPS}}
|COMPS] }}).
lexicon(れる,
word&{'PHONOLOGY':[れる],
'SYN':{'HEAD':動詞&{'FORM':終止&},
'COMPS':[{'SYN':{'HEAD':動詞&{'FORM':未然&},'COMPS':COMPS}}
|COMPS] }}).
9-2-7.LiLFeS と AZ-Prolog の型付素性構造の違い
型システムの位置づけ
LiLFeS では全ての定数が型として扱われます。つまり、
% LiLFeS | ?- X = 二等辺三角形, X = 直角三角形.
のような例に登場する「二等辺三角形」「直角三角形」はそれぞれ二等辺三角形型、直角三角形型の値として扱われます。また、数字や文字列も型を持ちます。たとえば、数字の 12 は 12 型の値であり、これは integer 型の subtype でもあります。同様に、文字列 "ABC" は "ABC" 型の値であり、これは string 型の subtype でもあります。リストもまた、 list 型の subtype です。さらに、述語も pred 型の subtype という位置づけになっています。
AZ-Prolog においても LiLFeS と同様の型システムをサポートしていますが、 AZ-Prolog におけるデータのすべてが LiLFeS における型に対応するわけではありません。AZ-Prolog ユーザーズマニュアル 4-1.Prologのデータ構造 にあるように AZ-Prolog はさまざまな種類のデータ構造を取り扱うことができますが、これらのデータ構造は型付素性構造を除き、 LiLFeS に相当する意味での型を備えていません。
AZ-Prolog で LiLFeS 互換の型を表現するためには、型付素性構造モードにおいて、型名の後ろに '&' を付ける必要があります。次の例では、二等辺三角形型と直角三角形型の単一化を行っています。
% AZ-Prolog | ?- X = 二等辺三角形&, X = 直角三角形&. % 型の単一化
一方で、次の例は AZ-Prolog においては「二等辺三角形」というアトムと「直角三角形」というアトムの単一化とみなされてしまいます。
% AZ-Prolog | ?- X = 二等辺三角形, X = 直角三角形. % アトム同士の単一化 (失敗する)
また、 AZ-Prolog では型付素性構造モードにおいても数字、文字列、リストは AZ-Prolog 自体に備わったデータ型として扱われ、 LiLFeS のような意味での型を直接備えているわけではありません。つまり、厳密にいえば数字の 12 は integer 型の subtype という扱いにはなっていません。ただし、素性定義の際に素性値の型を integer 型とした場合、その素性に対応する値には任意の整数を持たせることができる仕様となっているため、 LiLFeS と等価なプログラムを書くことが可能です。
% AZ-Prolog でコンサルトすると型検査を通る
a <- [bot] + [f:integer].
p :- X = a&{f:12}, write(X), nl.
integer 型以外にも float 型、string 型、list 型、atom 型が同様の仕組みを備えています。特に、アトムおよびそれに対応する atom 型は AZ-Prolog にだけ備わっており LiLFeS には存在しません。
なお、 AZ-Prolog では述語は型を持ちませんので、 pred 型の subtype として定義する必要はありません (pred 型という組み込み型は存在しません) 。
型・素性・変数の書式
型名として使える文字列は、LiLFeS と AZ-Prolog で基本的に同様です。英小文字またはかな漢字で始まる文字列、それに加えてシングルクォーテーション (') で囲んだ文字列を用いることができます。
素性名に関しても AZ-Prolog では型名と同じ種類の文字列が利用可能です。LiLFeS においては英大文字で始まる文字列も素性名とすることができますが、 AZ-Prolog ではこのような文字列はシングルクォーテーションで囲む必要があります。
変数に関しては、 AZ-Prolog では (型付素性構造以外の場合と同様に) 英大文字またはアンダーライン ( _ ) で始まる文字列が利用可能です。LiLFeS では $ で始まる文字列も変数として用いることができますが、 AZ-Prolog では用いることができません。
型付素性構造の書式
AZ-Prolog の場合、型付素性構造の書式は
型&{素性1:素性1の値, 素性2:素性2の値, ...}
となります。これと同じ構造を LiLFeS で書くと
型 & 素性1¥素性1の値 & 素性2¥素性2の値 & ...
となります。AZ-Prolog では素性と素性値の区切りにデフォルトではコロン (:) を用いますが、この記号は fs_delimiter/2
述語で変更可能です。以下に素性構造が入れ子状になった場合の例を示します。AZ-Prolog で
a&{p:b&{q:c&, r:d&}, s:{t:e&}}
となる構造は、 LiLFeS だと
a & p¥(b & q¥c & r¥d) & s¥t¥e
と表されます。
型・素性定義の書式
AZ-Prolog で型と素性の定義を行うための構文は次の通りです。
型 <- [型1, 型2, ...] + [素性1:素性1の型, 素性2:素性2の型, ...].
LiLFeS での対応する構文ではコロン (:) の代わりにバックスラッシュ (¥) を用いる点が異なります。
LiLFeS の仕様のうち、次のものは AZ-Prolog では実装されていません。
- ・親となる型が 1 つの場合、型名の左右の [ ] を省略できる
- ・素性値の型が bot の場合は省略できる
- ・素性の表示順序を指定できる
モジュール
LiLFeS と異なり、 AZ-Prolog ではモジュール名の宣言を行う必要はありません。